Addition Strategies

When young children first start to add and subtract they have to model every part of the problem. This stage of development is known as Direct Modeling. For a problem like 6+5, a direct modeler would count out 6 objects, count out 5 objects, and then recount them all starting back at 1. This is an important stage of development and allows children lots of practice with counting and one-to-one tagging (tagging each object with only one number name), however we do not want children to stay in this stage for long.

Watch examples of children in the Direct Modeling Stage:

Watch examples of children in the Counting Stage:

After direct modeling, children progress into the Counting stage. Unfortunately this is the stage that too many children get stuck in and never quite move out of. For the problem 6+5, a counter would hold the “6” in their head and count on from there. We tend to move children straight from counting to just memorizing their facts. However, if a child cannot remember a certain fact they slide back down to the counting stage. Instead of jumping straight to memorizing facts after the counting stage, research shows that if you help children develop flexibility and relationships around facts the memorization will come naturally after this Derived Fact stage. Derived facts are when kids use facts they know to help them with facts they do not know. While kids are in the counting stage we should be providing them with manipulatives like Ten Frames and MathRacks which help children see these derived facts:

Using Doubles
The doubles facts (2+2, 3+3, etc.) tend to be the first facts that kids have memorized. These facts happen in nature and we see them in our daily lives. Helping kids connect the symbolic fact to things they see in everyday life will help these facts become easily recalled. Here are just a few ideas:

1+1 are the front and back wheel of a bicycle
2+2 are the 2 wheels in front and back of a 4-wheeler
3+3 are the legs on insects
4+4 are the legs on a spider
5+5 are their fingers on each hand
6+6 are eggs in a dozen
7+7 are the days in two weeks or football scores
8+8 are crayons in a 16 count box or the number of pawns in a chess game
9+9 are the wheels on an 18-wheeler truck or holes on a golf course
10+10 are your fingers and toes

Watch this video of 3rd, 2nd, and 1st graders using Doubles facts to help them with other facts.

Making 10
Because 10 is such an integral part of our number system, it is essential that children know the numbers that combine together to make 10 (which then helps them as they get to multi-digit numbers and making the next “10”, i.e. 43 + 7 makes 50). Using manipulatives like the Ten Frames or MathRacks help children see how many more to make 10 as they are adding numbers. For instance, when solving 7 + 8 using the MathRack, children will move over the 7 beads and then they might see the 3 beads remaining on the top row to make a full row of 10 and then add 5 more on the bottom row:

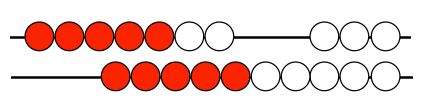
Watch this video of 3rd & 2nd graders using Make 10 facts to help them with other facts.

Finding Fives
This strategy hasn’t become as popular as Doubles and Make 10 in textbooks, but children invent this strategy on their own when they use manipulatives like Ten Frames and MathRacks. The picture below is using Ten Frames to show 6 + 7:

Kids who use Ten Frames and MathRacks begin to see the groups of 5 within each number. So to solve 6+7, they pull out the two full rows of 5 to make 10 and then add the extra 1 and 2 from the bottom rows.

Watch this video of 2nd & 3rd graders Finding Fives to help them with other facts.

Ten plus Something
These facts are essentially understanding the teen numbers (10+1, 10+2, 10+3, etc.). When kids see these problems they should instantly know the answer because our teen numbers are just ten plus some more. However, too many kids count on to solve these problems. One of the issues comes from our words for these numbers; eleven, twelve, and thirteen do not help children see the 10 and some more in the number. The words for 11, 12, 13, etc in some other languages are actually their words for 10 and 1, 10 and 2, etc. This starts those kids off from the beginning with the understanding that 11 is 10 and 1. So, we have to do a lot to help children build that connection.

Watch this video of 1st, 2nd, & 3rd graders using, and not using, the 10 plus Something facts.